International Journal of Scientific & Engineering Research Volume 2, Issue 6, June-2011 1
ISSN 2229-5518
A Fuzzy Inference System for Synergy Estimation of Simultaneous Emotion Dynamics in Agents
Atifa Athar, M. Saleem Khan, Khalil Ahmed, Aiesha Ahmed and Nida Anwar
Abstract— This paper presents that emotions manifest the information processing mechanism of human mind that infers the synergic effect of simultaneous emotions to achieve focused communication and decision making. This proposed work considers integration mechanism of complex emotional dynamics for agents to communicate reason and decide in conflicting situations like humans. The proposed inference system is used to estimate the blended effect of simultaneously activated emotions in agents using fuzzy logic as it is an unsurpassed choice to deal with uncertain information and classification of non- deterministic events.
Index Terms— Fuzzy inference, Simultaneous emotion dynamics, Synergy estimation, blended emotions, PAD, W heel of emotions, social cohorts.
—————————— • ——————————
motional intelligence corresponds to the awareness and usage of emotions to make smart decisions in different situations. The segregation between an intelligent and
non-intelligent mind is based on awareness that is an out- come of inference and regarding psychological viewpoint emotions are well thought out as inferential shortcuts [1].
An emotion is not an isolated feature of human mind; it is to be considered as a variable in nature. It grows or decays temporally due to the change in the environmen- tal information absorbed by mind. Since this information is not always discrete and certain thus it may cause simul- taneous emotion activation in mind. The dynamic me- chanism of human mind can have a variety of emotional states simultaneously and can convey their shared or di- verse effect [2]. To infer these effects it is required to blend these simultaneously active emotions. There could be one of the four varieties i.e. quick succession, superpo- sition, masking and suppression that are plausible to the phenomenon of blended emotions [3].
To measure the blended effect of simultaneous emo- tions it is important to capture their properties. Each emo- tion is unique and can be distinguished in terms of their
————————————————
• Ms. Atifa Athar is working as a faculty member at the School of Computer Science, NCBA&E Lahore, Pakistan. She is a research fellow at SCS, NCBA&E (e-mail: atifaathar@yahoo.com)
• Dr. M. Saleem Khan is with the Computer Science Department as Director in GC University Lahore, Pakistan (e-mail: mskgcu@yahoo.com).
• Dr. Khalil Ahmed is with the School of Computer Science at NCBA&E Lahore, Pakistan, He is an expert academician and passionately engaged in research. (e-mail: drk@ncbae.edu.pk).
• Ms. Aiesha Ahmad is with Computer Science department as research fellow
at NCBA&E Lahore, Pakistan (e-mail: aiesha@ncbae.edu.pk).
• Ms. Nida Anwar is with Computer Science department as research fellow
at NCBA&E Lahore, Pakistan. She is currently working as faculty member in VU, Lahore, Pakistan (e-mail: nidaanwar85@gmail.com)
dynamic properties i.e. intensity, valence and dominance.
Therefore, fear, anger, sadness, and disgust are nega-
tive primary emotions while happiness and surprise are
positive ones. Scherer modeled emotions as a continuous
progression in three-dimensional space that consists of
Pleasure/Valence (P), representing the overall valence
information, Arousal (A), accounting for the degree of activeness of an emotion, and Dominance/ Power (D), describing the experienced “control” over the emotion itself or the situational context [4].
The association between primary emotions caters the possibility of complex or secondary emotions. The dynamics of secondary emotions emerged from the asso- ciation of primary emotions and experience [5], which are possible to be mapped along the PAD coordinates for example, smugness might be considered a blend of the two elemental emotions: happiness, and contempt [6].
The fuzzy theory has been used recently by different researchers in emotion modeling for artificial agents. Arief has discussed visualization of emotional facial ex- pression using Naive Bayes and Fuzzy logic [7]. Elisabetta presented an embodied conversational agent to show complex emotional facial expression[8].
Emotions are an important feature of non-verbal HCI. Ayesha has presented her research work in this area us- ing rough fuzzy sets to resolve the complexity [9]. A fuzzy emotion model VISBER is presented by Natascha that is applicable for the real time facial emotion recogni- tion in agents [10]. One of the advantages of Fuzzy logic includes that it captures the changes smoothly from the environment and generate even output instead of crisp values [11].
This research paper proposes an inference system us- ing the fuzzy logic to process the dynamics of simulta- neously active emotions and estimates their mixed effects
IJSER © 2011 http://www.ijser.org
International Journal of Scientific & Engineering Research Volume 2, Issue 6, June-2011 2
ISSN 2229-5518
or transitional succession. The output of the system could be used in artificial agency for the decision making etc.
The emotionless agents are simply considered as ma- chines and not trustworthy for humans [12]. Therefore, in accordance with human psychology, the role of agents as our future social cohorts suggests that these are required to be equipped with integrated mechanism of complex emotional dynamics to communicate reason and decide in conflicting situations like humans.
This paper is structured as follows: Section 2 elaborates the approach adopted for emotion blends. Section 3 ex- plains the fuzzy logic scheme. Section 4 argues about the fuzzy rule base scheme to infer the blended effect of si- multaneous emotions. Section 5 provides the comparison of Matlab simulated and calculated results. Section 6 con- cludes this work and suggests some possible future direc- tions.
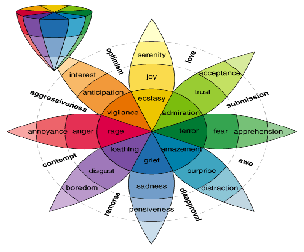
According to evolutionary and developmental psycholo- gy it is known that a human mind may not experience just one basic emotion at a time rather it feels simultane- ous or complex emotions while sensing the environmen- tal events. The term “basic” has been used to describe elements that combine to form more complex or com- pound emotions for example, smugness might be consi- dered a blend of the two elemental emotions, happiness, and contempt.[6] Considering psycho-evolutionary theory of emotions articulated by Plutchik there are eight primary emotions in humans i.e. anger, anticipation, joy, trust, fear, surprise, sadness and disgust,. Fig 1 presents the Plutchik’s complete scheme of human emotions hav- ing eight basic emotions as “Wheel of Emotions”. [13]
nations of neighboring pairs of emotion on the wheel e.g. trust and fear leads to submission. The primary blend of eight basic emotions is presented in table I.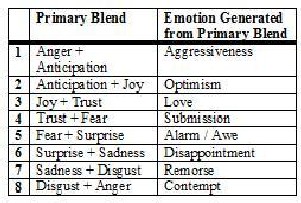
Likewise secondary dyad combines two emotions with the gap of one emotion on the wheel and produces the complex emotions from primary ones as presented in ta- ble II.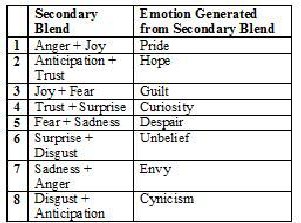
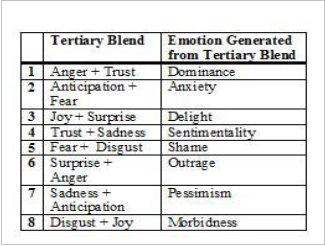
The tertiary dyad combines emotions with the gap of two emotions on the Wheel, presented in table III.
The blend of emotions at three different levels could be achieved through primary, secondary and tertiary dyads on the Wheel. [14] Each primary dyad shows the combi-
IJSER ©
International Journal of Scientific & Engineering Research Volume 2, Issue 6, June-2011 3
ISSN 2229-5518
Fuzzy logic is based on Boolean logic and works with partially true or false values. The fuzzy systems deals with the truth values in Fuzzy logic or membership val- ues in fuzzy sets that are indicated by a value on the range [0.0, 1.0], with 0.0 representing absolute Falseness and 1.0 representing absolute Truth.[15]
From the literature it is clear that an emotion’s attributes are usually not represented by crisp values rather these have fuzzy boundaries. Therefore, we propose a fuzzy inference system with the classification of primary emo- tional states that blends their intensities together and con- stitute the secondary emotion. The design of proposed system is represented in Fig. 2.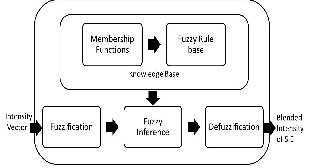
4.1 Fuzzification of Emotion Intensities
The fuzzification process is used to transform the crisp values of emotion intensities into degrees of membership for linguistic terms of fuzzy sets. We are considering the primary emotion identified by Plutchik represented in table IV as input to the proposed fuzzy inference system.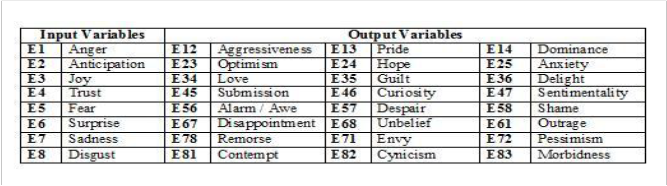
In the proposed scheme, we are assuming that the in- tensity of an emotion can be mapped to the interval [0, 1]. The following linguistic variables have been chosen for fuzzification of input intensities and divided into three types based on probability values of intensities of all eight primary emotions.
a. Low: 0.0 – 0.5
b. Medium:0.3 – 0.7
c. High: 0.5 – 1.0
These linguistic variables are used to decide the degree of membership in fuzzification set. The plot of member- ship functions for one of the fuzzy input variables is represented in Fig. 3.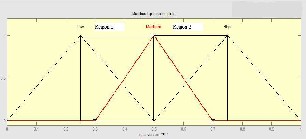
The three membership functions, f1 [1] for Low, f1 [2] for Medium, and f1 [3] for High are used to show the var- ious ranges of input fuzzy variable “E1” in a plot consist- ing of two regions as shown in Fig. 3. The number of membership functions and range values for each of the fuzzy input variables are taken same as E1,……..,E8 are representing the intensity of primary emotions.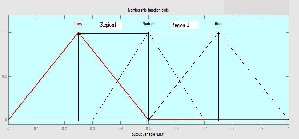
International Journal of Scientific & Engineering Research Volume 2, Issue 6, June-2011 4
ISSN 2229-5518
For generalization, the range values of each output membership function plot are taken same. Therefore, the shape of the plot for each output variable, used in design is the same and shown in Fig. 4.The proposed system consists of eight input variables and their values may lie in any one of the two regions as listed in Table V.
The linguistic values are the plotting values of the fuzzy input variables with the membership functions employed in different regions. As eight variables are used, therefore sixteen linguistic values are represented in Fig. 5.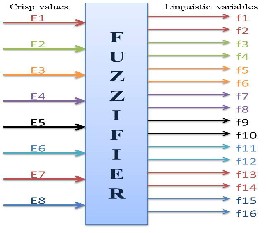
The mapping of input fuzzy variables with the mem- bership functions in two regions is listed in Table V.
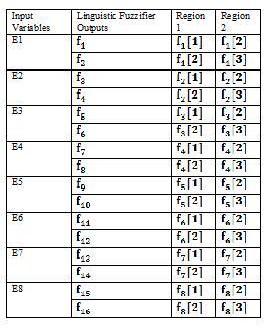
Both of the regions are divided in two halves and each region consists of two membership functions at a time.
4.2 Fuzzy Inference Engine
After determining the degree of membership in the fuzzi- fication process the subsequent step is to make linguistic rules to decide that which secondary emotion will be gen- erated in response to the inputs provided to the system.
In inference process the value of intensity given to each emotion synergies and estimates the intensity of the sec- ondary emotion produced with the help of inference rules. On the basis of number of inputs and linguistic va- riables, the number of fuzzy rules is determined.
In reference to the “Wheel of emotions” it is observed that secondary emotions cannot be highly intense rather these could be produced with medium intensity by blend- ing two highly intense primary emotions. And if primary emotions are blended with medium intensity then the secondary emotion produced is comparatively less in- tense.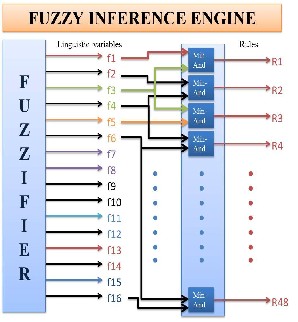
In our proposed system there are 8 input variables i.e. E1, E2, ………, E8 and 3 linguistic variables therefore by using AND connector it is possible to have 6561 rules, but in reference to the combinations of emotions presented in table I, II, III only 24 combinations i.e. E12 . . . . . . . E83 presented in table IV have been chosen to design the infe- rence rules. These combinations cater the blend of only two primary emotions at three different levels.
The fuzzified intensity of emotions E1 …… E8 is pro- vided as input to each rule and the intensity of one of the relevant secondary emotion provided in table 5 is pro- duced.
IJSER © 2011 http://www.ijser.org
International Journal of Scientific & Engineering Research Volume 2, Issue 6, June-2011 5
ISSN 2229-5518
For example the inference rules could be
• If E1 is Medium AND E2 is Medium THEN E12 is
Low
• If E6 is High AND E7 is High THEN E67 is Me-
dium
There are 48 rules that has been used for 24 combina- tions because of the usage of AND connector that caters the minimum value of variables.
The inference engine contains 48 AND gates, it accepts sixteen inputs from the fuzzifier and produce R values by applying min-max composition. Each rule takes two in- put values, synergies these and inferences the final output using min-AND operation. Following is the calculation of R values from some of the selected rules out of 48 rules with the values E1 = 0.65, E2 = 0.7, E8 = 0.7, E3 = 0.6 in region2.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() = = 0.6 0.8 = 0.6
= = 0.6 0.8 = 0.6 ![]()
![]()
![]() = = 0.4 0.2 = 0.2
= = 0.4 0.2 = 0.2
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() = = 0.4 0.8 = 0.4
= = 0.4 0.8 = 0.4 ![]() = = 0.6 0.2 = 0.2
= = 0.6 0.2 = 0.2
By applying the Mamdani-min process we get the min-
imum value from the membership function values using
AND operation. The sign ^ between the membership
function values represents the Min-ANDing process.
4.3 Rule Selector
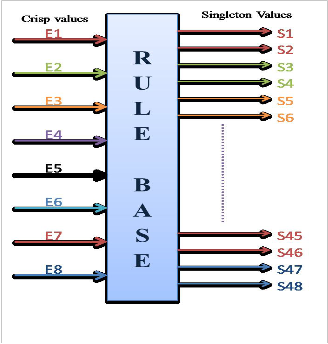
The rule base works with eight crisp input values, di- viding the universe of discourse into two regions, each containing two fuzzy variables, fires the rules, and gives the output singleton values corresponding to each output variable as presented in Fig. 7.
The rule selector for the proposed system receives eight crisp values from the input variables. It provides singleton values of output functions according to the for- ty eight rules. According to the division of the regions for each output variables there are forty eight singleton val- ues S1, S2, S3, ……., S48.
4.4 Defuzzification
After the estimation of inputs the defuzzification process generates the crisp values for output variables. In the proposed system there are 96 inputs that are provided to each of 48 defuzzifiers, forty Eight values of R1,R2,……..,R48 from the outputs of inference engine and forty eight singleton values S1, S2, ………,S48 from the rule selector as shown in Fig.7. Each defuzzifier estimates the crisp value output according to the center of average (C.O.A) method using the mathematical expression, L: Si * Ri I L: Ri, where i = 1 to 48.
S1 = 0.25
S2 = 0.5
S3 = 0.75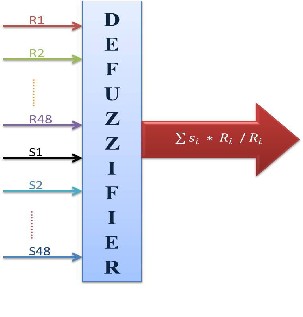
![]()
![]()
![]()
![]()
![]()
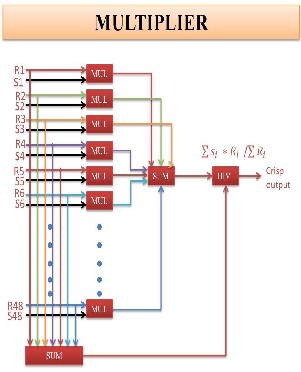
The design formation of defuzzifier is represented in Fig. 9. Each defuzzifier consists of 48 multipliers for ![]()
![]() one adder to sum up, one adder for and one divider for to provide the final estimated output crisp value.
one adder to sum up, one adder for and one divider for to provide the final estimated output crisp value.
IJSER © 2011 http://www.ijser.org
International Journal of Scientific & Engineering Research Volume 2, Issue 6, June-2011 6
ISSN 2229-5518
The results calculated from the fuzzy inference engine![]()
![]()
![]()
![]()
+
Two output variables E12 and E83 have been chosen for the comparisons. The crisp values for E12 and E83 are determined using mathematical expression L: Si *Ri I L: Ri from the values of the input variables that are provided in the fuzzy inference process.
These calculated results according to the system design are compared with the results according to the MATLAB simulation in Table VI and found correct. Fig. 10 represents the input variables & Fig. 11 represents the output variables from the Rule Viewer in MATLAB.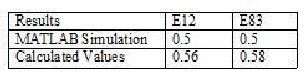

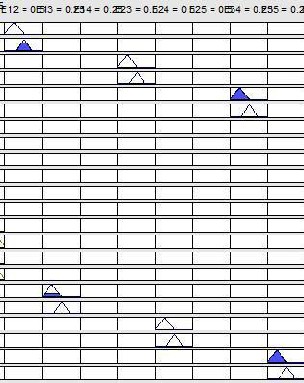
Figure 11: MATLAB Rule Viewer for Output Va- riables
IJSER © 2011 http://www.ijser.org
International Journal of Scientific & Engineering Research Volume 2, Issue 6, June-2011 7
ISSN 2229-5518
Following is one of the simulated graphs for output E12 for the proposed inference system according to the values of E1 and E2 provided for inference process mentioned above.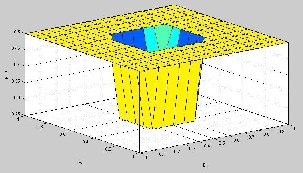
Figure 12: Plot between E1 and E2
There are several emotion inference systems presented by researchers but these do not infer and verify the coex- istence of numerous emotions and their blends according to Plutchik theory of emotional blend. However our pro- posed fuzzy inference system estimates the synergy of two emotions that activates simultaneously quite effi- ciently.
The comparisons between calculated and simulated values afford it a role in estimation authenticity for blended emotions.
The proposed system design and simulation work could also lead to the new avenues in the field of model- ing complex emotion dynamics for agency.
[1] P. Scaruffi. The Nature of Consciouss. 2006, ISBN 0976553112
[2] G-Y. Park, S-I. Lee W-Y. Kwon and J-B. Kim. “Neurocogni- tive Affective System for an Emotive Robot”. Proceedings of IEEE/RSJ International Conference on Intelligent Robot and Systems (pp. 2595 - 2600). Beijing: IEEE, China, 2006.
[3] S. Buisine, S. Abrilian, R. Niewiadomski, J. Martin, L. Devillers,
and C. Pelachaud, “Perception of Blended Emotions: from Vid- eo Corpus to Expressive Agent”. Proceedings of 6th International Conference on Intelligent Virtual Agents (IVA 2006). 4133/2006, pp. 93-106. Marina Del Rey, CA, USA: Springer Berlin / Hei- delberg, August 10, 2006.
[4] C. Becker-Asano, I. Wachsmuth. “Virtual Humans Growing up: From primary toward Secondary Emotion”. Autonomous Agents and Multi-Agent Systems, 20(1), pp. 32 – 49, 2009.
[5] L.Custodio, R.Ventura, and C. P.Ferreira. “Artificial Emotions
and Emotion-Based Control Systems.” Proceedings of 7th IEEE
International Conference on Emerging Technologies and Factory Au- tomation .( ETFA), 2, pp. 1415 - 1420. Barcelona 1999.
[6] P. Ekman. Basic Emotions. In Handbook of Cognition and Emotion.
Sussex, U.K.: John Wiley & Sons, 1999.
[7] M. Arief, M. I. Wardhana, S. Sumpeno, and M. Hariad. “Emo- tion Expression of Three Dimensional Face Model Using Naive Bayes and Fuzzy Logic.” International Journal of Computer Science and Network Security (IJCSNS), 10(5), May 2010.
[8] E. Bevacqua, M. Mancini, R. Niewiadomski and C. Pelachaud. “An expressive ECA showing complex emotions.” Proceedings of Artificial and Ambient Intelligence.(AISB, 07). Newcastle Uni- versity, Newcastle upon Tyne, UK, 2007.
[9] A. Butalia, A. R Ramani, and P. Kulkarni. “Emotional Recogni- tion and towards Context based Decision.” International Jour- nal of Computer Applications, 9(3), pp. 42 – 54, November
2010.
[10] N. Esau, E. Wetzel, L. Kleinjohann, B. Kleinjohann, “Real-Time Facial Expression Recognition Using a Fuzzy Emotion Model." IEEE International Conference In Fuzzy Systems, (pp. 1 - 6), 2007.
[11] H. Mobahi, S. Ansari. “Fuzzy Perception, Emotion and Expres- sion for Interactive Robots.” IEEE International Conference on Systems, Man and Cybernetics, 2003 .
[12] L .PourMohammadBagher. “Intelligent Agent System Simula- tion Using Fear Emotion.” World Academy of Science, Engi- neering and Technology 48, 2008.
[13] R. Plutchik and H. Kellerman. Emotion: Theory, research, and experience. Newyork, USA: Academic Press, 1983.
[14] J. Turner. Origin of Human Emotions: A Sociological Inquiry into the Evolution of Human Affect, Stanford University Press, 2000.
[15] M. Hellmann. Fuzzy Logic Introduction. Epsilon Nought Radar
Remote Sensing Tutorials, 2001.
IJSER © 2011 http://www.ijser.org